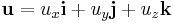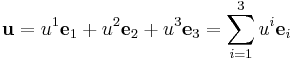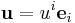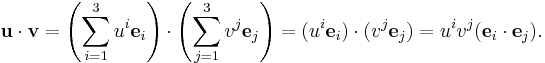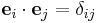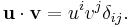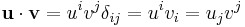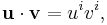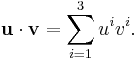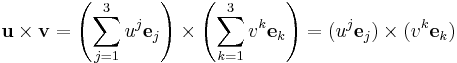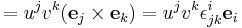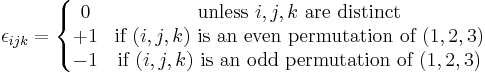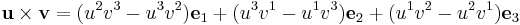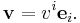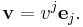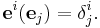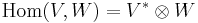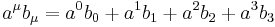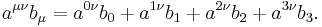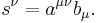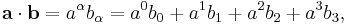Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae. It was introduced by Albert Einstein in 1916.[1]
According to this convention, when an index variable appears twice in a single term it implies that we are summing over all of its possible values. In typical applications, the index values are 1,2,3 (representing the three dimensions of physical Euclidean space), or 0,1,2,3 or 1,2,3,4 (representing the four dimensions of space-time, or Minkowski space), but they can have any range, even (in some applications) an infinite set. Thus in three dimensions
actually means
The upper indices are not exponents, but instead different axes. Thus, for example, 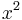 should be read as "x-two", not "x squared", and corresponds to the traditional y-axis. This use of Abstract index notation is a way of presenting the summation convention so that it is made clear that it is independent of coordinates.
should be read as "x-two", not "x squared", and corresponds to the traditional y-axis. This use of Abstract index notation is a way of presenting the summation convention so that it is made clear that it is independent of coordinates.
In general relativity, a common convention is that the Greek alphabet and the Roman alphabet are used to distinguish whether summing over 1,2,3 or 0,1,2,3 (usually Roman, i, j, ... for 1,2,3 and Greek, 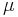 ,
, 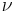 , ... for 0,1,2,3).
, ... for 0,1,2,3).
Einstein notation can be applied in slightly different ways. Often, each index must be repeated once in an upper (superscript) and once in a lower (subscript) position; however, the convention can be applied more generally to any repeated indices.[2] When dealing with covariant and contravariant vectors, where the indices also indicate the type of vector, the first notation must be used; a covariant vector can only be contracted (summed) with a contravariant vector. On the other hand, when there is a fixed coordinate basis (or when not considering coordinate vectors), one can work with only subscripts; see below.
Introduction
Example of Einstein notation for a vector:
In Einstein notation, vector indices are superscripts (e.g. 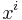 ) and covector indices are subscripts (e.g.
) and covector indices are subscripts (e.g.  ). The position of the index has a specific meaning. It is important, of course, not to confuse a superscript with an exponent—all the relations with superscripts and subscripts are linear, they involve no power higher than the first. Here, the superscripted i above the symbol x represents an integer-valued index running from 1 to n.
). The position of the index has a specific meaning. It is important, of course, not to confuse a superscript with an exponent—all the relations with superscripts and subscripts are linear, they involve no power higher than the first. Here, the superscripted i above the symbol x represents an integer-valued index running from 1 to n.
The virtue of Einstein notation is that it represents the invariant quantities with a simple notation.
The basic idea of Einstein notation is that a vector can form a scalar:
This is typically written as an explicit sum:
This sum is invariant under changes of basis, but the individual terms in the sum are not. This led Einstein to propose the convention that repeated indices imply the sum:
This, and any, scalar is invariant under transformations of basis. When the basis is changed, the components of a vector change by a linear transformation described by a matrix.
As for covectors, they change by the inverse matrix. This is designed to guarantee that the linear function associated with the covector, the sum above, is the same no matter what the basis is.
Vector representations
In linear algebra, Einstein notation can be used to distinguish between vectors and covectors.
Given a vector space  and its dual space
and its dual space 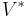 :
:
Vectors 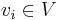 have lower indices
have lower indices 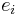 , and components of vectors (i.e. coordinates of vector endpoints) have upper indices
, and components of vectors (i.e. coordinates of vector endpoints) have upper indices 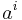 .[Note] So a vector
.[Note] So a vector  with an index of
with an index of  is expressed as:
is expressed as:
where 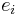 is a basis for
is a basis for  .
.
Covectors 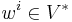 have upper indices
have upper indices 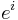 , and components of covectors have lower indices
, and components of covectors have lower indices 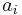 .[Note] So a covector
.[Note] So a covector  with an index of
with an index of  is expressed as:
is expressed as:
where 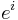 is the dual basis for
is the dual basis for 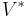 .
.
Note that 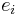 is a vector,
is a vector, 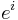 is a covector, and
is a covector, and 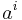 and
and 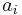 are scalars. The product returns a vector
are scalars. The product returns a vector  or covector
or covector  , respectively. Since basis vectors
, respectively. Since basis vectors 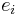 are given lower indices and coordinates are labeled with upper indices
are given lower indices and coordinates are labeled with upper indices 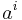 , summation notation suggests pairing them (in the obvious way) to express the vector.
, summation notation suggests pairing them (in the obvious way) to express the vector.
In a given basis, the coefficient of 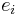 (which is
(which is 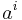 ) is the value of the covector in the corresponding dual basis:
) is the value of the covector in the corresponding dual basis: 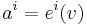 .
.
In terms of covariance and contravariance of vectors, upper indices represent components of contravariant vectors (vectors), while lower indices represent 'components' of covariant vectors (covectors): they transform covariantly (resp., contravariantly) with respect to change of basis. In recognition of this fact, the following notation uses the same letter both for a (co)vector and its components, as in:
Here 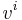 means the components of the vector
means the components of the vector  , but it does not mean "the covector
, but it does not mean "the covector  ". It is
". It is  which is the covector, and
which is the covector, and 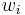 are its components.
are its components.
Mnemonics
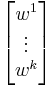
In the above example, vectors are represented as (n,1) matrices "column vectors", while covectors are represented as (1,n) matrices "row covectors". The opposite convention is also used. For example, the DirectX API uses row vectors.[3]
When using the column vector convention
- "Upper indices go up to down; lower indices go left to right"
- You can stack vectors (column matrices) side-by-side:
Hence the lower index indicates which column you are in.
- You can stack covectors (row matrices) top-to-bottom:
Hence the upper index indicates which row you are in.
Superscripts and subscripts vs. only subscripts
In the presence of a non-degenerate form (an isomorphism 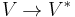 , for instance a Riemannian metric or Minkowski metric), one can raise and lower indices.
, for instance a Riemannian metric or Minkowski metric), one can raise and lower indices.
A basis gives such a form (via the dual basis), hence when working on 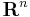 with a Euclidian metric and a fixed orthonomal basis, one can work with only subscripts.
with a Euclidian metric and a fixed orthonomal basis, one can work with only subscripts.
However, if one changes coordinates, the way that coefficients change depends on the variance of the object, and one cannot ignore the distinction; see covariance and contravariance of vectors.
Common operations in this notation
In Einstein notation, the usual element reference 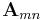 for the
for the  th row and
th row and  th column of matrix
th column of matrix 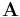 becomes
becomes 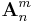 . We can then write the following operations in Einstein notation as follows.
. We can then write the following operations in Einstein notation as follows.
Inner product
Given a row vector  and a column vector
and a column vector  of the same size, we can take the inner product
of the same size, we can take the inner product 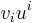 , which is a scalar: it's evaluating the covector on the vector.
, which is a scalar: it's evaluating the covector on the vector.
Multiplication of a vector by a matrix
Given a matrix 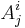 and a (column) vector
and a (column) vector 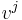 , the coefficients of the product
, the coefficients of the product 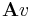 are given by
are given by 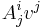 .
.
Similarly, 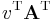 is equivalent to
is equivalent to 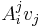 .
.
But, be aware that: notations like 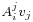 are somewhat misleading, then they are refined to
are somewhat misleading, then they are refined to
to keep track of which is column and which is row. In the notations: 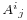 , the index
, the index  (the first index) is row, and the index
(the first index) is row, and the index  (the second index) is column.
(the second index) is column.
Matrix multiplication
We can represent matrix multiplication as:
This expression is equivalent to the more conventional (and less compact) notation:
Trace
Given a square matrix 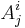 , summing over a common index
, summing over a common index 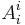 yields the trace.
yields the trace.
Outer product
The outer product of the column vector u by the row vector ' ' yields an M × N matrix A:
' yields an M × N matrix A:
In Einstein notation, we have:
Since i and j represent two different indices, and in this case over two different ranges M and N respectively, the indices are not eliminated by the multiplication. Both indices survive the multiplication to become the two indices of the newly-created matrix A of rank 1.
Given a tensor field and a basis (of linearly independent vector fields), the coefficients of the tensor field in a basis can be computed by evaluating on a suitable combination of the basis and dual basis, and inherits the correct indexing. We list notable examples.
Throughout, let 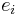 be a basis of vector fields (a moving frame).
be a basis of vector fields (a moving frame).
- (covariant) metric tensor
- (contravariant) metric tensor
- Torsion tensor (using the below)
which follows from the formula
This also applies for some operations that are not tensorial, for instance:
where 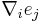 is the covariant derivative. Equivalently,
is the covariant derivative. Equivalently,
- commutator coefficients
where ![[e_i,e_j]](/2012-wikipedia_en_all_nopic_01_2012/I/c55ca28badbdb98ee8862a3f5dca38ac.png) is the Lie bracket. Equivalently,
is the Lie bracket. Equivalently,
Vector dot product
In mechanics and engineering, vectors in 3D space are often described in relation to orthogonal unit vectors i, j and k.
If the basis vectors i, j, and k are instead expressed as e1, e2, and e3, a vector can be expressed in terms of a summation:
In Einstein notation, the summation symbol is omitted since the index i is repeated once as an upper index and once as a lower index, and we simply write
Using e1, e2, and e3 instead of i, j, and k, together with Einstein notation, we obtain a concise algebraic presentation of vector and tensor equations. For example,
Since
where 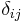 is the Kronecker delta, which is equal to 1 when i = j, and 0 otherwise, we find
is the Kronecker delta, which is equal to 1 when i = j, and 0 otherwise, we find
One can use 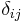 to lower indices of the vectors; namely,
to lower indices of the vectors; namely, 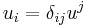 and
and 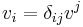 . Then
. Then
Note that, despite 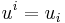 for any fixed
for any fixed  , it is incorrect to write
, it is incorrect to write
since on the right hand side the index  is repeated both times as an upper index and so there is no summation over
is repeated both times as an upper index and so there is no summation over  according to the Einstein convention. Rather, one should explicitly write the summation:
according to the Einstein convention. Rather, one should explicitly write the summation:
Vector cross product
For the cross product,
where 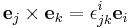 and
and 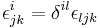 , with
, with 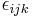 the Levi-Civita symbol defined by:
the Levi-Civita symbol defined by:
One then recovers
from
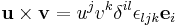
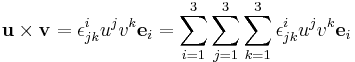 .
.
In other words, if 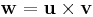 , then
, then 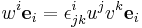 , so that
, so that 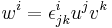 .
.
Abstract definitions
In the traditional usage, one has in mind a vector space  with finite dimension n, and a specific basis of
with finite dimension n, and a specific basis of  . We can write the basis vectors as e1, e2, ..., en. Then if '
. We can write the basis vectors as e1, e2, ..., en. Then if ' ' is a vector in
' is a vector in  , it has coordinates
, it has coordinates  relative to this basis.
relative to this basis.
The basic rule is:
In this expression, it was assumed that the term on the right side was to be summed as i goes from 1 to n, because the index i does not appear on both sides of the expression. (Or, using Einstein's convention, because the index i appeared twice.)
An index that is summed over is a summation index. Here, the i is known as a summation index. It is also known as a dummy index since the result is not dependent on it; thus we could also write, for example:
An index that is not summed over is a free index and should be found in each term of the equation or formula if it appears in any term. Compare dummy indices and free indices with free variables and bound variables.
The value of the Einstein convention is that it applies to other vector spaces built from  using the tensor product and duality. For example,
using the tensor product and duality. For example,  , the tensor product of
, the tensor product of  with itself, has a basis consisting of tensors of the form
with itself, has a basis consisting of tensors of the form 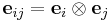 . Any tensor
. Any tensor 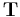 in
in  can be written as:
can be written as:
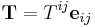 .
.
V*, the dual of  , has a basis e1, e2, ..., en which obeys the rule
, has a basis e1, e2, ..., en which obeys the rule
Here δ is the Kronecker delta, so 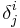 is 1 if i =j and 0 otherwise.
is 1 if i =j and 0 otherwise.
As
the row-column coordinates on a matrix correspond to the upper-lower indices on the tensor product.
Examples
Einstein summation is clarified with the help of a few simple examples. Consider four-dimensional spacetime, where indices run from 0 to 3:
The above example is one of contraction, a common tensor operation. The tensor 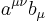 becomes a new tensor by summing over the first upper index and the lower index. Typically the resulting tensor is renamed with the contracted indices removed:
becomes a new tensor by summing over the first upper index and the lower index. Typically the resulting tensor is renamed with the contracted indices removed:
For a familiar example, consider the dot product of two vectors a and b. The dot product is defined simply as summation over the indices of a and b:
which is our familiar formula for the vector dot product. Remember it is sometimes necessary to change the components of a in order to lower its index; however, this is not necessary in Euclidean space, or any space with a metric equal to its inverse metric (e.g., flat spacetime).
See also
- Abstract index notation
- Bra-ket notation
- Penrose graphical notation
- Kronecker delta
- Levi-Civita symbol
Notes
- This applies only for numerical indices. The situation is the opposite for abstract indices. Then, vectors themselves carry upper abstract indices and covectors carry lower abstract indices, as per the example in the introduction of this article. Elements of a basis of vectors may carry a lower numerical index and an upper abstract index.
References
- ^ Einstein, Albert (1916). "The Foundation of the Gen eral Theory of Relativity" (PDF). Annalen der Physik. http://www.alberteinstein.info/gallery/gtext3.html. Retrieved 2006-09-03.
- ^ "Einstein Summation". Wolfram Mathworld. http://mathworld.wolfram.com/EinsteinSummation.html. Retrieved 13 April 2011.
- ^ Dunn, Parberry (2002). 3d Graphics Primer for Graphics and Game Development. Wordware. pp. 90–91.
Bibliography
- Kuptsov, L.P. (2001), "Einstein rule", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=E/e035220.
External links
- Rawlings, Steve (2007-02-01). "Lecture 10 - Einstein Summation Convention and Vector Identities". Oxford University. http://www-astro.physics.ox.ac.uk/~sr/lectures/vectors/lecture10final.pdfc.
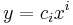
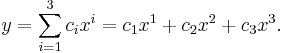
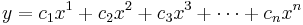
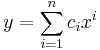
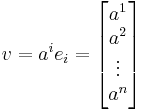
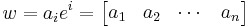
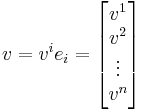
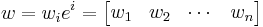

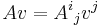
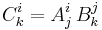
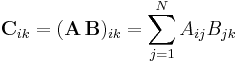
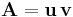
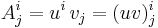
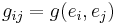
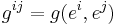
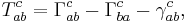
![T = \nabla_X Y - \nabla_Y X - [X,Y].](/2012-wikipedia_en_all_nopic_01_2012/I/e68c00b5b7fb4e22c63954088ed58024.png)

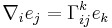
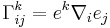
![[e_i,e_j] = \gamma_{ij}^k e_k](/2012-wikipedia_en_all_nopic_01_2012/I/b7da2745ba44a5444bdde15530effa6c.png)
![\gamma_{ij}^k = e^k[e_i,e_j].](/2012-wikipedia_en_all_nopic_01_2012/I/5780a0b24e8526482b5e77ab9567b185.png)